Dans ce TP, vous allez utiliser un outil qui sait resoudre des problèmes de type Boolean satisfyability (SAT) afin de prouver l’équivalence de deux circuits logiques.
1. Problème à resoudre
Nous disposons de fichiers dans un format simple représentant des circuits logiques au niveau des portes. Il existe différents formats de ce type (comme BLIF, EDIF, …) utilisé par des outils de synthèse ou de simulation. Ces formats sont souvent pas très lisible, surtout pas pour un humain. Pour être sûr que la synthèse et l’optimisation n’ont pas introduit d’erreurs (ce qui est tout à fait possible), on utilise des outils de preuve d’équivalence (equivalence checker). Par exemple, pour vérifier un nouveau type d’additionneur optimisé, on prouve qu’il est équivalent à un circuit bien connu comme un simple carry ripple adder.
Pour effectuer la preuve d’équivalence, vous allez vous servir d’un solveur de satisfiabilité (SAT solver). Un tel outil est capable de répondre à la question suivante:
Pour une formule logique en CNF (conjunctive normal form), est-ce qu’il existe une affectation des variables tel que la formule est vraie?
Afin de pouvoir utiliser un SAT solver pour notre preuve, il faut donc trouver un moyen d’exprimer notre problème de départ comme un problème SAT. Globalement, le but de ce TP est d’implementer le design pattern encode – solve – decode de la manière suivante:

En fait, pendant ce TP, vous allez seulement vous occuper du côté encodage, car le décodage de la solution est plus ou moins trivial.
2. Mise en place de l’environnement de développement
Récupérez les sources du TP:
git clone git@gitlab.enst.fr:se206/tp-satec.git
Pour resoudre les dépendences de paquets Python, exécutez la commande suivante:
cd tp-satec ./deps.sh
Pour voir si tout s’est bien passé, exécutez le script de test:
./examples.py
S’il y a un problème, allez voir les encadrants. Le script example.py contient des exemples d’usages des modules fournis pour ce TP. Pour plus d’info sur l’API, vous pouvez vous servir de l’aide de Python:
irma@a405-03:~/tp-satec$ python3 Python 3.6.3 (default, Oct 3 2017, 21:45:48) [GCC 7.2.0] on linux Type "help", "copyright", "credits" or "license" for more information. >>> import circuit.circuit as circ >>> import circuit.cnf as cnf >>> help(circ) >>> help(cnf)
Important: Pensez à sauvegarder votre travail régulièrement (git add – commit). Le rendu du TP se fait via le Moodle. Pensez à écrire du code net et lisible. Pour cela, il est impératif de commenter votre code!
3. Circuits Logiques
Dans le dossier benchmarks, vous trouvez des exemples de fichiers qui démontrent le format textuel pour décrire des circuits logiques. La syntaxe exacte du format ne nous intéresse pas en détail, car nous disposons d’un parseur qui fera le travail de lecture pour nous. Un circuit a
- Des entrées
- Des sorties
- Des signaux internes
- Des équations Booléennes qui définissent le comportement du circuit
Tous les signaux sont de type Boolean, il n’y a pas d’entier ou de vecteur de bits. Un circuit est en fait un graphe acyclique orienté (DAG, directed acyclic graph), dont les racines sont les entrées est le feuilles les sorties. Le schéma suivant montre le graphe d’un additioneur (full adder). Le fichier d’origine est benchmarks/fa.crc:
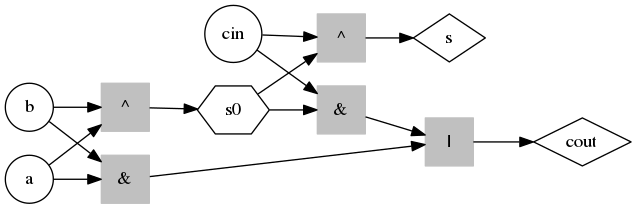
On voit les entrées (a, b, cin), les sorties (s, cout), un signal interne (s0) ainsi que des portes (&, ^, |). En fait, la représentation du circuit vu en haut ne correspond pas complètement à la structure de la classe Circuit, car il n’y a pas de connexion entre la porte XOR à gauche et le signal interne s0. Un objet de type Circuit contient plutôt un dictionnaire associant les noms des signaux internes à des noeds dans le graphe, et le graphe lui-même contient un noed de type Variable avec le nom de la variable interne s0.
Le script examples.py contient du code pour lire le fichier et pour lancer une simulation du circuit. La fonction dot() d’un circuit produit une représentation sous forme de graphe dans le format graphviz. Vous pouvez en faire une image avec l’outil dot:
dot -Tpng fa.dot > fa.png
4. Conjunctive Normal Form
L’autre module fourni pour ce TP permet d’écrire des expressions logiques en CNF, et de les donner à un SAT solver pour trouver une affectation qui valide l’expression (ou de prouver qu’il n’existe pas de telle affectation). Regardez dans le script examples.py pour voir comment écrire une CNF et comment la resoudre à l’aide de l’API Solver.
Rappelez-vous les définitions sur le problème SAT présentés pendant le cours. En particulier, la notion de la transformation Tseitin nous sera très utile pour ce TP. Pendant le cours, il a été démontré comment obtenir une formule CNF équisatisfiable pour une porte OR.
Les circuits traités pendant ce TP sont composés de quatre types de portes logiques:
- Les portes OR (ou)
- Les portes AND (et)
- Les portes NOT (inverseur)
- Les portes XOR (ou exclusif)
1. Développez les transformations manquantes pour les portes AND, NOT et XOR. Dans le fichier adder.py, rajoutez des fonctions qui réalisent ces transformations.
2. Dans le fichier adder.py, construisez une expression CNF pour l’additioneur, suivant la transformation Tseitin.
Utilisez le SAT solver pour obtenir une solution de la CNF. À quoi correspond une solution?
5. Transformation Automatique
Maintenant, on voudrait automatiser la transformation d’un circuit suivant la transformation Tseitin. Pour cela, vous allez implémenter une fonction en Python qui prend en entrée un circuit (voir la classe Circuit) et qui génère une expression logique en CNF.
3. Ouvrez le fichier transform.py et implementez la fonction transform(). Testez votre code avec les exemples fournis. En particulier, le script test.py sert à évaluer votre code.
Il va falloir traverser la structure du graphe pour transformer chaque noed du circuit. Pour la transformation, il est très utile d’avoir un identifiant unique pour chaque noed afin de stocker et de retrouver les variables pour la CNF. Pour les noeds internes, vous pouvez utiliser la fonction getID() qui vous donne un tel identifiant (un entier). Voir aussi le script examples.py pour des exemples d’usage de la structure d’un circuit.
Une exigence pour la CNF résultante est que pour tous les signaux nommés (entrées, sorties, signaux internes), les noms des variables SAT correspondantes soient identiques aux noms des signaux du circuit. Si la fonction transform() est appelée avec un prefix non vide, il faut que toutes les variables portent ce préfix.
Par exemple, soit un circuit C avec une sortie ‘sum’, nous construisons la CNF:
cnf = transform(C, prefix='foo_')
Supposons que le solver SAT nous donne une solution pour cette CNF:
solver = Solver() solution = solver.solve(cnf)
On peut ensuite récupérer la valeur que le solveur à trouvé pour la sortie ‘sum’:
sum = solution['foo_sum']
6. Preuve d’Équivalence
Dans cette étape de ce TP, vous allez vous servir de la transformation Tseitin pour réaliser un equivalence checker (EC). Comme expliqué pendant le cours, on peut combiner deux circuits qui ont la même interface d’une telle manière que la sortie du circuit combiné nous indique si les circuits donnent des résultats différents pour une affectation donnée des entrées:
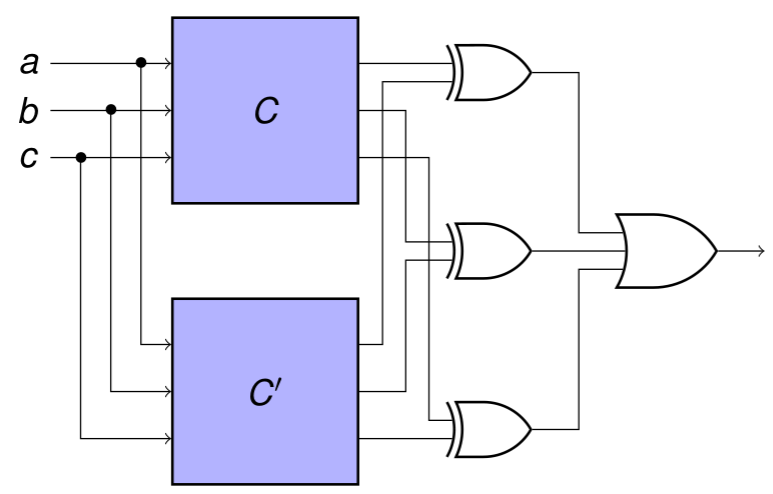
Le terme anglais pour ce circuit est miter. Au lieu de simuler ce circuit pour toutes les entrées possible (ce qui prendra beaucoup de temps), on utilise la transformation Tseitin et un SAT solver. La question d’équivalence devient donc:
Est-ce qu’il existe une affectation des entrées de notre miter tel que la seule sortie du circuit prend la valeur 1?
Si elle existe, il s’agit d’un contre-exemple qui démontre la non-équivalence. Sinon, les circuits sont vraiment équivalent. Pour réaliser notre EC, il suffit donc de
- Faire une transformation Tseitin des deux circuits,
- « Connecter » les entrées correspondantes (comment exprimer cela en CNF?)
- rajouter la logique de comparaison du miter, et
- rajouter une contrainte sur la sortie pour la forcer à 1 (comment exprimer cette contrainte en CNF?).
4. Ouvrez le fichier ec.py et implementez la fonction check().
La fonction check() prend en entrée deux circuits. La fonction doit retourner une pair de valeurs dont la première sera True en cas d’équivalence et False en cas de non-équivalence. La deuxième sera None en case d’équivalence, sinon elle donne la solution trouvée par le SAT solver. Si vous constatez la non-équivalence sans faire appel au SAT solver (par exemple, si les entrées/sorties des circuits ne sont pas compatibles), vous pouvez retourner (False, None).
Attention: La fonction SatVar(‘x’) donne toujours le même objet si vous l’appelez plusieurs fois avec le même identifiant ‘x’. Cela peut être très utile, mais il faut faire attention quand vous faites les transformations pour deux circuits qui ont les mêmes noms d’entrées et de sorties. Utilisez le prefix dans la signature de la fonction transform() pour créer des noms de variables uniques pour chaque circuit.
Testez votre EC avec le script test.py.
7. Rendu du TP
Vous avez jusqu’au 28 février pour compléter ce TP. Les solutions aux questions 1, 2, 3 et 4 seront notées (fichiers adder.py, transform.py et ec.py).
Important: La soumission de votre solution se fait par le Moodle. Pour cela, faites un dernier commit et exportez votre code vers une archive portant votre nom:
git commit -m "final version" git archive --output NomPrenom.tar master
